如何选择特征?熵与信息增益 Entropy & Information Gain
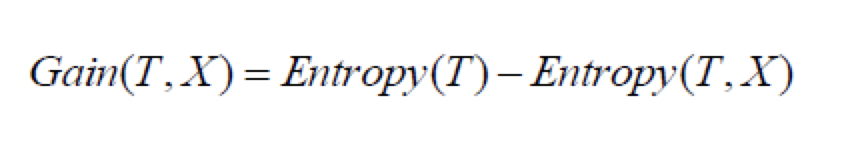
特征工程是整个推荐算法开发过程中比较重要的环节,如何在海量特征中找到有效的特征,可以利用决策树的细想,决策树本身就是通过信息增益(ID3),信息增益比(C4.5),基尼系数(CART)来选择最优特征来作为叶子结点,本文主要介绍如何通过计算 信息增益 来进行特征选择。
熵(香农熵)Shannon Entropy
熵 表示随机变量不确定性的度量。
熵的本质是表示系统内的混乱程度,引申到样本集中来看,如果一组样本集的应变量越“多样”,则“熵”最大,反之如果一组样本集中的硬变量越“纯净”,则“熵”最小。
在信息论中的熵也被称为香农熵,对应公式为:
$$ Ent(D)=-\sum_{k=1}^y p_k\log_2p_k $$
Ent(D) 的值越小,则表示样本 D 的“纯度”越高。
举例来看
第一种情况:随机抛一枚硬币,理论上抛到正反面的概率各为 50%,我们就可以知道投一次硬币的熵为:
$$ Ent(投硬币)=-\frac{1}{2}\times\log_2\frac{1}{2}-\frac{1}{2}\times\log_2\frac{1}{2} \ = -(\frac{1}{2}\times-1)-(\frac{1}{2}\times-1) = 1 $$
第二种情况:假设一枚硬币质地不合格,投正面的概率是 80%,投背面的概率是 20%,那么它的熵为:
$$ Ent(投硬币)=-\frac{4}{5}\times\log_2\frac{4}{5}-\frac{1}{5}\times\log_2\frac{1}{5} = 0.7219 $$
第三种情况:如果投正面的概率为 100%,背面的概率是 0%,那么它的熵为:
$$ Ent(投硬币)=-1\times\log_21-0\times\log_20 = 0 $$
所以在这个事件中,投硬币的熵,反应了投硬币这个事件的不确定性,如果是一枚正常的硬币,他投出来正反面的“不确定”就越大,对应的熵也就越大。
如果一个事件服从伯努利分布(二项分布),那么他的概率与熵的对应关系呈下图的关系:
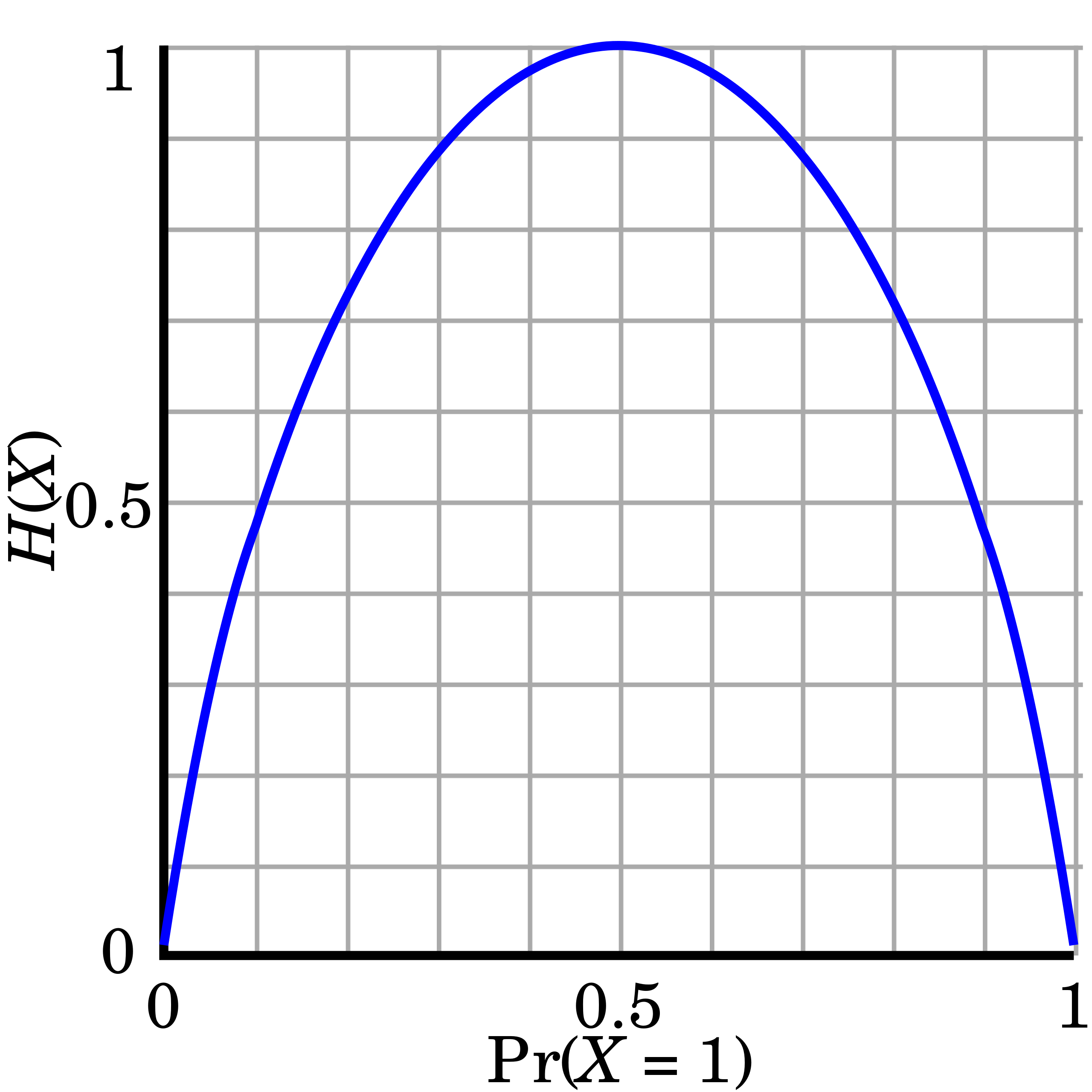
条件熵 Conditional Entropy
知道熵的概念,我们再来理解条件熵,条件熵的定义是:条件熵描述了在已知第二个随机变量 X 的值的前提下,随机变量 Y 的信息熵还有多少。简单地说,条件熵表示在 X 条件下 Y 的信息熵。公式如下:
$$ Ent(Y|X)=\sum_{x\in{X}}p(x)Ent(Y|X=x) $$
我们还是来举个例子,看下面这个测试数据集 10 条数据,其中 5 条为点击样本,5 条为未点击样本
| 用户id | 视频id | 是否点击 | 用户地区 | 视频类别 |
|---|---|---|---|---|
| 754 | 1 | 是 | 杭州 | 搞笑 |
| 755 | 2 | 否 | 杭州 | 搞笑 |
| 756 | 3 | 是 | 宁波 | 搞笑 |
| 757 | 4 | 否 | 宁波 | 搞笑 |
| 758 | 5 | 是 | 杭州 | 搞笑 |
| 759 | 6 | 否 | 宁波 | 搞笑 |
| 760 | 7 | 是 | 杭州 | 搞笑 |
| 761 | 8 | 否 | 宁波 | 电视剧 |
| 762 | 9 | 是 | 杭州 | 搞笑 |
| 763 | 2 | 否 | 杭州 | 电视剧 |
该样本的信息熵为:
$$ Ent(点击样本)=-\sum_{k=1}^y p_k\log_2p_k = -\frac{1}{2}\times\log_2\frac{1}{2}-\frac{1}{2}\times\log_2\frac{1}{2} = 1 $$
设地区为随机变量 X,是否点击作为样本的随机变量 Y,则:
$$ p(X=宁波)= \frac{4}{10} = \frac{2}{5} $$
$$ p(X=杭州)= \frac{6}{10} = \frac{3}{5} $$
所以
$$ Ent(Y|X)=\sum_{x\in{X}}p(x)Ent(Y|X=x) $$
$$ = p(X=宁波)\times Ent(Y|X=宁波) + p(X=杭州)\times Ent(Y|X=杭州)$$
根据上面讲到的 信息熵 的计算方法:
$$ Ent(Y|X=宁波)= -\sum_{k=1}^y p_k\log_2p_k $$
$$ = -(p(Y=点击|X=宁波) \times \log_2p(Y=点击|X=宁波)) $$
$$ - (p(Y=未点击|X=宁波) \times \log_2p(Y=未点击|X=宁波)) $$
其中:
$$ p(Y=点击|X=宁波) = \frac{1}{4} $$
$$ p(Y=未点击|X=宁波) = \frac{3}{4} $$
所以上述公式:
$$ Ent(Y|X=宁波) = -(\frac{1}{4}\times \log_2\frac{1}{4} + \frac{3}{4}\times \log_2\frac{3}{4}) $$
$$ = 0.811 $$
同理继续求:
$$ Ent(Y|X=杭州) = -\sum_{k=1}^y p_k\log_2p_k $$
$$ = -(p(Y=点击|X=杭州) \times \log_2p(Y=点击|X=杭州)) $$
$$ - (p(Y=未点击|X=杭州) \times \log_2p(Y=未点击|X=杭州)) $$
$$ = -(\frac{4}{6}\times \log_2\frac{4}{6} + \frac{2}{6}\times \log_2\frac{2}{6}) $$
$$ = 0.918 $$
因此:
$$ Ent(Y|X)=\sum_{x\in{X}}p(x)Ent(Y|X=x) $$
$$ = p(X=宁波)\times Ent(Y|X=宁波) + p(X=杭州)\times Ent(Y|X=杭州)$$
$$ = \frac{2}{5}\times 0.811 + \frac{3}{5} \times 0.918 = 0.8752 $$
至此我们求得了当「地区」维度作为已知条件时,样本的信息熵,可以看到熵从 1 下降到 0.8752,说明如果我们知道「地区」这个变量时,样本的“纯度”会升高,不确定性会“下降”。
信息增益 Information Gain
理解了信息熵和条件熵,信息增益就很好理解了,信息熵表示了样本的不确定性的程度,条件熵表示已知某个条件下,样本的不确定性的程度。那么他们两个差值,就表示已知某个条件时,会“降低”整体样本的不确定性的程度,这个“降低”的程度对应的值,就是信息增益的值,公式为:
$$ Gain(D,X) = Ent(D) - Ent(D|X) $$
举例可知上述的数据集,「地区」对样本的信息增益为:
$$ Gain(点击, 地区) = Ent(点击样本) - Ent(点击样本|地区) = 1 - 0.8752 = 0.1248 $$
特征选择 Feature Selector
之后就是工程上重复的步骤,计算每个特征维度对样本的「信息增益」,我们就可以得出每个维度特征对样本的「信息增量」,然后从大到小排序,取前 N 个特征,我们就可以达到利用「信息增益」来进行特征选择目的。
试试上述数据集中,「视频类别」所产生的信息收益!
Reference
- 信息熵和条件熵的计算 CSDN
- 熵 (信息论) 维基百科
- 机器学习 - 周志华 - 决策树章节
